Разработка стратегий НЛП и использование их в образовательной деятельности.
ИЛИ
Процедура внутреннего управления ориентировочной деятельностью и использование ее в алгоритмизации действий.

В. Лебедев, (Москва)

В этой статье мы хотим поделиться с учителями, специалистами в области НЛП разработанными и апробированными стратегиями моделирования не только различных образовательных видов деятельности, но и деятельности направленной на решение различных житейских проблем.

Для неискушенного в терминологии читателя мы хотим, предварительно, пояснить, что любая человеческая деятельность состоит как минимум из трех частей: ориентировочной, исполнительной и контролирующей. В зависимости от того, на сколько точно и эффективно будет реализована ориентирующая составляющая деятельности на столько полноценно и эффективно она может быть исполнена.

В качестве примера мы предлагаем вам решить следующую задачу:

Представьте, что вы проснулись среди ночи в полной темноте. Вам необходимо одеться, не включая свет. Как вы это сделаете, если ваша одежда лежит рядом с кроватью?
Опишите процесс, так чтобы любой другой человек мог его повторить, понимая при этом, почему производится то или иное действие.

Когда Вы все это сделаете, переместитесь на третью страницу и сравнить Ваш вариант решения с нашими предложениями, но предварительно прочитайте страницу 2.

Прежде, чем перейти к следующей странице ответьте на вопрос, когда человек начинает думать, когда возникает сам акт мышления, что ему должно предшествовать?

Люди начинают думать тогда, когда задают себе вопрос (или он возникает, не осознано или им его задают) и начинают искать на него ответ.

Великий Эйнштейн как-то сказал: - если бы мне стало известно, что на меня готовится покушение, и до его исполнения остался час, то я бы потратил 55 минут на то, чтобы правильно сформулировать вопрос и 5 минут на то чтобы решить эту проблему.

Как вы понимаете новое?

Первое, что вы делаете, это ставите перед собой вопрос ЧТО ЭТО? или КТО ЭТО? или ЧТО ЭТО ЗНАЧИТ? И, наверное, это один из самых важных вопросов. Так как, не зная, что перед вами, вы не сможете ни определить, что с ним можно делать, что нельзя, как к нему относится и стоит ли относится вообще. Но бывает, что вы не знаете что это? Тогда вы можете задать себе вопрос, а на что это похоже? И ответ, подскажет вам, в каком направлении думать дальше.

Представьте, что Вы никогда не видели крокодила, даже на картинке и никогда не слышали о нем и не знаете даже такого названия. Представьте, что вы оказались на берегу незнакомой реки в местности, достаточно жаркой и душной и наблюдаете некое длинное, зелёное, бревнообразное животное с мощным хвостом и длинной, вытянутой мордой, которая, учитывая её размер, может широко раскрыться. Весь ваш жизненный опыт, знание животного мира, какое бы оно у вас не было, заставят вас насторожится, и держатся от этого бревна подальше. Нет, конечно, есть и такие люди, которым захочется все-таки выяснить: что это? изучить так, сказать это поближе. Если такие и были, то, вряд ли они читают эти строки.

Какой же вопрос последует за первым вопросом ЧТО ЭТО?
Второй вопрос, - ЧТО Я ХОЧУ? относительно того, что передо мной. Так в случае крокодила, скорее, всего вам захочется быть от него подальше.
Обычно на пути реализации наших желаний встречаются препятствия, и поэтому третий вопрос звучит так: ЧТО МНЕ МЕШАЕТ? (Что мешает достичь желаемого? Что стоит на пути? Какая преграда?…)

Как вы думаете, каким должен быть следующий вопрос?

После того, как вы определите то, что вам мешает естественно задать себе вопрос, - КАК ИЗБАВИТСЯ? (Как избавится от того, что вам мешает?
И наконец, следующий вопрос - КАК ЭТО СДЕЛАТЬ?

Всмотритесь в эти пять вопросов

1. Что это? Кто это? Что это значит?
2. Что я хочу?
3. Что мне мешает?
4. Как избавится?
5. Как это сделать?

Прочитайте их и сравните с вашим ответом на поставленную выше задачу.

Так как вы читаете эти строки то, это означает, что вы уже решили задачу и прочитали вторую страницу, если это так, то сейчас просто получайте удовольствие, сверяя ваш вариант решения с нашим.

А.

1. Я беру вещь и задаю себе вопрос, ЧТО ЭТО? На ощупь определяю качество ткани и вспоминаю, что из такой ткани у меня была футболка. Это футболка.
2. ЧТО Я ХОЧУ? Я хочу её одеть.
3. ЧТО МНЕ МЕШАЕТ? Я не знаю где перёд футболки.
4. КАК ИЗБАВИТСЯ от этого незнания? Нужно определить перёд.
5. КАК ЭТО СДЕЛАТЬ? Найти бирку; противоположная сторона есть то, что нам нужно.
   Ищу бирку и одеваю футболку.

Б

1. Беру следующую вещь. ЧТО ЭТО? Качество ткани - может быть рубашка, могут быть брюки (сделаны из одинакового материала). НА ЧТО ПОХОЖЕ? Ощупываю вещь ищу какие-либо признаки: пуговицы, карманы, разрезы … . Нахожу что-нибудь и делаю предположение; скоре всего брюки. Ищу ещё какой-нибудь признак, чтобы подтвердить моё предположение. Нахожу, убеждаюсь в справедливости предположения. Одеваю, так как уже знаю, что я хочу. И т.д.

Мы предлагаем вам провести небольшой эксперимент, выберите три небольших, с вашей точки зрения, проблемы и примените к ним эти пять вопросов.

Необходимо отметить, что в основе рассматриваемой стратегии, назовем ее стратегией ориентирования, лежит психотерапевтическая стратегия Anne K. Entus перевода проблемного состояния пациента в желаемое состояние, которая, в свою очередь, была создана на базе стратегии "SCOR".

Рассмотрим стратегию ориентирования, которая состоит из пяти шагов, и поясним ее применение на конкретных примерах.

Стратегия ориентирования.

• Что это? или Что это значит? или На что это похоже?
• Что я хочу?
• Что мне мешает достичь того, что я хочу?
• Как избавится от того, что мешает?
• Как это сделать?

Первый шаг этой стратегии организует внимание на том, что за объект перед нами, выделяет в нашем внутреннем информационном пространстве некую область, ассоциирующуюся с представленным объектом. Визуальные, словесные, некие ощущения соответствующие всему тому, что связано с объектом, действия, которые можно совершать с объектом с его частями и т.д.

Второй шаг направляет внимание и, следовательно, наше мышление на то, что мы хотим видеть, слышать, иметь, каким должен быть результат преобразований этого объекта. Эта информация может задаваться либо извне, либо содержаться в нашем внутреннем информационном пространстве и может актуализироваться уже на первом шаге.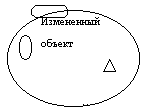

Третий шаг позволяет определить то, что требует изменений для перевода объекта из одного состояния в другое.

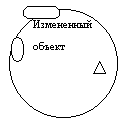
Четвертый шаг переводит фокус внимания к выделенным элементам, которые необходимо преобразовать и организует поиск средств для этого преобразования.
Пятый шаг дает возможность сосредоточится на организации системы перевода объекта в желаемое состояние.

При экспериментальном внедрении рассматриваемой стратегии ориентирования, в школах Москвы, мы вместе с учителями анализировали ответы учащихся с позиции того, что мешает им правильно решить поставленную перед ними задачу. Учителя самостоятельно отмечали, что пропуск того или иного шага стратегии ориентирования не давал возможность учащимся продвигаться в том направлении, которое бы позволило решить поставленную перед ними задачу.

То есть, на первом шаге это неправильное владение понятийным аппаратом темы либо неправильное подведение под понятие, либо отсутствие самого процесса определения, что за объект представлен перед учащимися. Как следствие, учащиеся были дезориентированы до тех пор, пока учитель наводящими вопросами не обращал их внимание на необходимость уточнения того, что же находится перед ними и т.д. Таким образом, учителя приходили к пониманию необходимости планомерного обучения школьников применению рассматриваемой стратегии. Кроме того, необходимость такого обучения заставляла самих учителей изменять свои стереотипы, которые они использовали при разработке и введении учебной информации искать другие пути конструирования своей деятельности.

Эффективное конструирование учебной деятельности школьников учителем возможно только при наличии в его внутреннем опыте соответствующих стратегий переработки информации. В качестве таких стратегий мы рассматриваем стратегию ориентации и моделирование пути достижения результата.

Ниже мы предлагаем вашему вниманию описание процедур позволяющих моделировать пути достижения результата, и рассматриваем их применение на конкретных примерах.

Моделирование пути достижения результата.

1. Сформулируйте результат. (здесь используются пять признаков хорошо сформулированного результата)
1. Определите, достижимы ли все признаки результата сразу или их нужно достигать по отдельности или какие-то вместе, а какие-то отдельно.
2. Задайте вопрос относительно сгруппированных признаков результата, - что нужно сделать, чтобы достичь его (их)? Ответьте на него.
   Ответ - нужно сделать "А".
3. Задайте вопрос относительно "А". Сделав это (А), достигну ли я признака результата, непосредственно? Если ответ отрицательный, то шаг 3а. Если положительный, то шаг 4.
1. Задайте вопрос - чего, я достигну, сделав это?
   Ответ - я достигну "А1"
2. Повторите шаги 3а, 3б до получения ответа - сделав это, я непосредственно достигну признака (ов) результата.
   Шаги 3а и 3б позволяют уточнить промежуточные действия между признаками результата и сформулированным действием (А). Очень часто на начальных этапах обучения слушатели называли действие, которое не посредственно не приводило к достижению нужных признаков.
4. Задайте вопрос, - достаточно ли выполнить "А", чтоб достичь нужного результата?
   Ответ - нужно сделать ещё "В" и….
   Этот шаг даёт нам возможность уточнить необходимость, каких-либо действий параллельных действию (А).
5. (начинается повтор цикла -это вопрос 2) Задайте вопрос - что нужно сделать, чтобы достичь "А"? считая его промежуточным результатом.
   Ответ - нужно сделать "А¹"
   Сделав "А¹" достигну ли я "А"
   Если ответ отрицательный, то повторите шаги 3а и 3б. Повторите шаги 4,5,6 относительно "А¹", затем "А²"… до момента, когда вы исчерпаете возможность двигаться в направлении "Что нужно сделать, чтобы достичь …?" Т.е. возникает ситуация, которую можно обозначить словами - это уже есть.

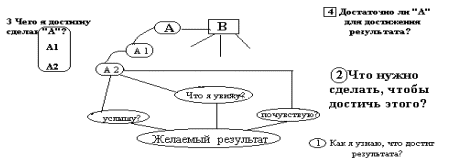
С помощью выше представленных процедур мы предлагаем вам определить путь решения такой образовательной задачи - обучающиеся умеют заваривать тонизирующий чай.

После того как вы определитесь с путем заваривания тонизирующего чая, можете перейти на страницу ниже.

Данная процедура показала свою эффективность в разработке общих и частных учебных алгоритмов. В качестве примера приведём процедуру, предложенную учителями начальной школы гимназии №1504, разработанную ими во время обучения. В качестве желаемого результата они выбрали: учащиеся заварили тонизирующий чай.

1. Желаемый результат - учащимися заварен тонизирующий чай.
   Как они узнают, что заварен тонизирующий чай?
   Они увидят цвет тонизирующего чая, почувствуют особый запах и вкус.
• Это все можно достичь практически вместе.
2. Что, нужно сделать, чтобы достичь этого?
   Ответ - правильно заварить чай.
3. Если они правильно заварят чай, достигнут ли они результата? Ответ - да, но при условии….
   Достаточно ли правильно заварить чай, чтоб он был тонизирующим?
   Ответ - нет. Нужно ещё правильно выбрать чай.

Схематично это было оформлено так, как показано ниже.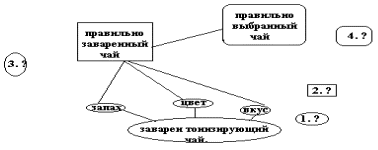

Рассмотрим несколько примеров такого конструирования.

Перед учителями естественно-научных циклов, участниками образовательных экспериментов, была поставлена следующая проблема - дана текстовая задача, на основании стратегии ориентации и моделирования пути достижения результата они должны были построить общие процедуры ее решения. Мы приводим повторение учителями, одной из разработок автора, которая относится к конструированию обобщенного подхода к анализу и решению текстовых задач. Что это?

Это может быть задача на движение, работу, проценты, сплавы и т.д. Здесь естественно возникает вопрос, как узнать то, что эта задача принадлежит к тому или иному классу задач. Этот вопрос относится к работе с понятийным аппаратом (конструирование панятийного аппарата учебных можно посмотреть в нашей брошюре "Как стать эффективным администратором и учителем" издательство «Первое сентября».

Что мы (я) хочу?

Решить задачу.

Переформулируем это высказывание с позиции результата. Нами (мной) решена задача.

Как мы (я) узнаем, что задача решена? Мы увидим правильный ответ, увидим правильно найденные соотношения между известными и неизвестными величинами. Что нам (мне) мешает достичь этого?

• Незнание участников задачи - тех, кто участвует в движения, в работе, из чего состоят сплавы смеси и т.д.
• Незнание компонентов описывающих процессы, происходящие с каждым участником - скорость, время, путь; производительность, время, произведенный объем работы и т.д.
• Незнание общих взаимосвязей между компонентами каждого участника - S = V·t; V = T·t; и т.д.
• Незнание изменений, соответствующих им состояний в описываемом движении, работе и т.д.
• Незнание взаимосвязей между компонентами каждого участника в каждом состоянии.
• Незнание взаимосвязей между компонентами участников в каждом состоянии.
• Незнание взаимосвязей между компонентами участников в разных состояниях.
• Незнание значений всех компонентов.

Как избавится от этого?
Узнать всю информацию по выше перечисленным 8 позициям.
Как это сделать?
Освоить соответствующую теорию. Проанализировать текст задачи по определенной системе. Используя найденные взаимосвязи вычислить значения необходимых компонентов.

Ниже мы приводим нашу статью, опубликованную в математическом приложении к газете «Первое сентября».

Анализ и решение текстовых задач.

Алгоритмизация

В школьном курсе математики решение текстовых задач считается одним из самых сложных для восприятия и усвоения учащимися разделов. С нашей точки зрения это связано с не разработанностью аналитического аппарата, который бы позволял рассматривать любую текстовую задачу как систему, в независимости от того, является ли она задачей на движение, на работу, на смеси или сплавы, на проценты и т. д.

Итак, для того, чтобы рассматривать задачу как систему, нам необходимо определить:

• элементы задачи;
• характер взаимосвязей между элементами.

Первый набор элементов, который необходимо определить в задаче как системе - это участники контекста задачи (машина и велосипед, поезда, амфибии и самолеты; рабочие и землеройки, станки и роботы; сплавы цинка и меди, раствор соли и спирта и т. д.)

Действие, производимое участником или с участником, в свою очередь также является системой. Эти действия определяются следующими элементами, которые называются компонентами:

• скорость V, время t, путь S - движения;
• производительность T, время t, объем работы V - работы;
• объем смеси V0, объем вещества в смеси Vв, объемная концентрация вещества в смеси cв, процентная, объемная концентрация вещества в смеси p^в% - смеси, сплава, раствора... ;
• и т.д.

По условиям задачи происходят различные изменения в значениях компонентов участников или накладываются на них какие-либо ограничения: увеличилась или уменьшилась скорость движения, известно время до встречи; вначале работали вместе, затем увеличилась производительность труда и т. д. Каждое такое изменение характеризует свою систему, состоящую из участников и соответствующих значений компонент. Назовем эти системы состояниями.

Тогда общую систему задачи можно представить в виде:

Структура системы определяется характером взаимосвязи между элементами. Таким образом, для полного раскрытия системы задачи нам необходимо определить взаимосвязи:

1. Между компонентами каждого участника в каждом состоянии.
   Назовем их вертикальными взаимосвязями. Почему именно так, будет видно из ниже рассматриваемых задач.
2. Между компонентами участников в каждом состоянии.
   Назовем их горизонтальными взаимосвязями или уравнивающими.
3. Между компонентами каждого участника в различных состояниях.
4. Между компонентами участников в различных состояниях.

Необходимость поиска взаимосвязи между компонентами участников в каждом состоянии требует ввести еще один элемент в систему задачи. Назовем его взаимосвязь (или общее).

Теперь наша таблица системы задачи будет выглядеть следующим образом: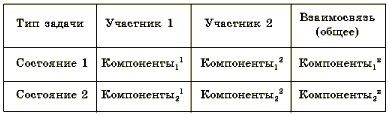

В зависимости от типа задачи таблица, описывающая ее систему, примет соответствующий вид. Например, для задачи на движение:

Движение каждого участника описывает три компоненты. Для того, чтобы найти взаимосвязь между ними, нам необходимо знать значения двух компонент. В традиционном подходе к решению текстовых задач для реализации этого положения вводятся неизвестные величины - x, y и т. д. Мы используем следующий подход. Пусть, например, S21 и S22 (указываем какие-либо из компонент) как будто бы известны и дальше работаем над задачей, исходя из этого.

Рассмотрим применение предлагаемого метода анализа и решения текстовых задач на конкретных примерах.

Задачи на движение²

Задача 1. Между домами Кролика и Лиса существовала прекрасная дорога в 50 км. Как-то так случилось, что они одновременно пошли друг к другу в гости. Они не пошли, а побежали. Через 5 часов, увлеченные воображаемым приятным времяпрепровождением в гостях, они пробежали мимо друг друга, рассеянно сказав: "Привет". Кролик, задумавшись над тем, неуловимо знакомым только что промелькнувшим мимо него, снизил свою скорость на 1 км/ч. Лис, почуяв что-то из того, что ему грезилось, увеличил скорость на 1 км/ч. Каково же было их разочарование, когда они не застали друг друга дома. У Лиса это разочарование наступило на 2 часа позже, чем у Кролика. С какой скоростью двигался Кролик?

Первым шагом анализа системы задачи мы определяем участников движения. Читаем текст задачи.

1. Сколько участников? - Два (Кролик и Лис).
   Вторым шагом определяем состояния: сколько их и какие они.
2. Сколько состояний? - Два (до встречи, после встречи).
   Третьим шагом изложим в таблице данные, необходимые для дальнейшего анализа системы задачи.

После построения таблицы еще раз читаем текст задачи (четвертый шаг) и заносим в нее данные значения компонентов.

Для удобства вашего восприятия при анализе этой задачи будем переходить от одной таблицы к другой, хотя в обычной ситуации весь анализ производится с помощью одной таблицы.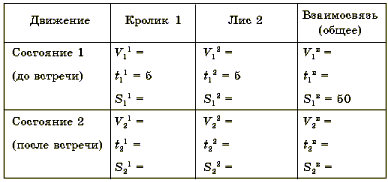

Для того, чтобы проанализировать первое состояние, нам необходимо ввести значения компонент, которые мы как бы знаем. Пусть это будет скорость кролика - V1. Тогда имеем (в скобках цифрами мы проставляем последовательность наших рассуждений):

(4) и (5) получены из анализа взаимосвязи компонентов каждого участника в различных состояниях и условия задачи. (6) и (7) - из анализа взаимосвязи компонентов участников в различных состояниях. (8) и (9) - из анализа взаимосвязи компонентов каждого участника в состоянии 2. (10) - из условия задачи.

На основании (10) имеем уравнение

решив которое получаем: V1 = 6 км/ч.

Ответ: 6 км/ч.

Можно отметить, что уравнения формируются из взаимосвязей между компонентами участников в состоянии. Поэтому мы и назвали их горизонтальными или уравнивающими

На учащихся производит большое впечатление, если они понимают, что для анализа системы задачи нет особой разницы в том, какой или какие значения компонентов принять за как бы известные величины. Еще больше их интригует возможность по полностью восстановленной системе задачи составлять свои задачи, переходить от одной задачи к другой.

Рассмотрим теперь задачу на работу, произведя анализ в одной таблице, нумеруя последовательность рассуждений цифрами в скобках.

Задача 2. Два тролля раскопают спрятанные в горе сокровища за 12 дней, работая вместе. Если же они будут работать по принципу: ты сделай половину, а потом я сделаю свою половину, то им потребуется 25 дней. Сколько дней потребуется каждому из них, чтобы в одиночку добраться до сокровищ?

(1) Сколько участников работы? - Два.
(2) Сколько возможных состояний в работе? - Три: а) совместная (параллельная) работа; б) поровну произведенная работа (последовательная работа); в) каждый сам за себя (индивидуальная работа).
(3) Значения величин, которые как будто бы даны T1 и T2.

Из рассуждения (10) с учетом (14) и (15) имеем:

Пустьтогда

Таким образом,

Ответ: 20, 30.

Рассмотрим задачу на сплавы и смеси.

Задача 3. Алиса, будучи в Зазеркалье, нашла две плошки смеси божьего дара с яичницей. Одна из них содержала a% божьего дара, а вторая - b%. В каком отношении Алиса должна взять эти смеси, чтобы при перемешивании получить новую смесь с массовым процентным содержанием божьего дара в g%?

Так как нас будет интересовать божий дар, то мы обозначим его - бд.

1. Сколько участников (сколько смесей участвует в задаче их названия)? - Три: смесь - 1, смесь - 2, новая смесь - 3.
2. Сколько состояний? - Одно.
3. Компоненты значения, которых как бы известны - масса первой m1⁰ и второй m2⁰ смеси, взятые для получения смеси с массовым процентным содержанием божьего дара в g%.

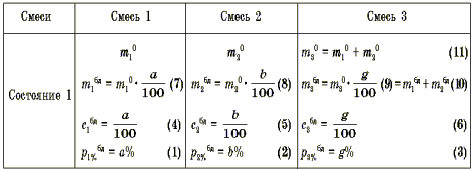Из (10), (9), (11) имеем: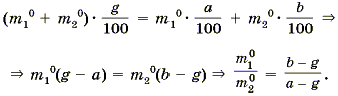

Мы не будем подробно останавливаться на анализе возможных значений a, b, g, так как это не является целью нашей статьи.

Таким образом, на рассмотренных задачах мы показали, как использовать метод анализа системы задачи, строить уравнения, которые приводят к решению текстовых задач.

Необходимо отметить, что данная методика обучения расширяет возможности учителя по развитию творческого мышления учащихся, позволяет развивать у них целостное и системное понимание математических закономерностей и взаимосвязей.

Ваши вопросы, предложения и пожелания Вы можете направлять по адресу: russc@soficom.com.eg

Дата последнего изменения: